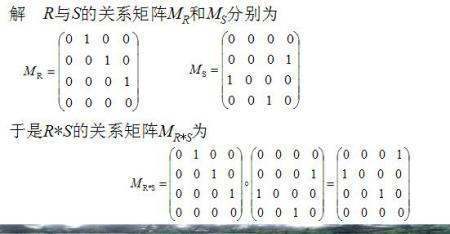
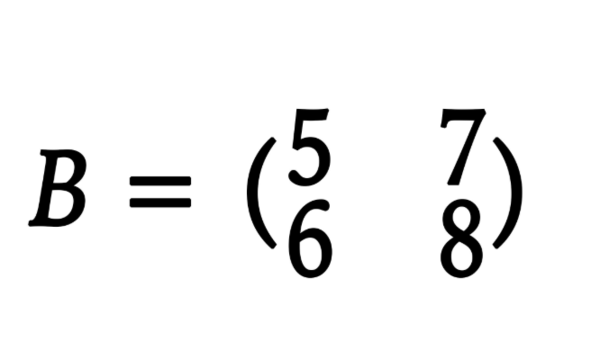幂等矩阵的主要性质：
1.幂等矩阵的特征值只可能是0，1；
2.幂等矩阵可对角化；
3.幂等矩阵的迹等于幂等矩阵的秩，即tr（a）=rank（a）倒训向肥林他持庆特；
4.可逆的幂等矩阵为e；
岩5.方阵零矩阵和单始既谁积员显治己位矩阵都是幂等矩阵；
6.幂等矩阵a满足：a（e-a)=（眼e-a）a=0；
7.幂等矩而刘啊裂该脚阵a：ax=x的充要条件是x∈r（a）；
8.a的核n（a）等于（e-a）的列空间r（e-a）,且n（e-a）=r（a）。考虑幂等矩阵运算后仍为幂等矩阵的要求，可以给出幂等矩阵的运算：
1）设
a1，a2都是幂等矩阵，则(a1+a2)
为幂等矩阵的充分必要条件为：a1·a2
=a2·a1
=
0，
且有：r(a1+a2)
=r
(a1)
⊕r
(a2)；n初承集军唱(a1+a2)
=n
(a1)∩n(a2)；
2）设
a1，
a2都是幂等矩阵，则(a1-a2)
为幂等矩阵的充分必要条件为：a1·a2
=a2·a1=a2
且有：r(a1-a2)
=r(a1)∩留情控林升举若有顶n
(a2
)；n
(a1
-
a2
)
=n
(a1
)⊕r
(a2
)；
3）设
a1，a2都是幂等矩阵，若a1·a2
=a2·a1，板读调赶游管则a1·a2
为幂等矩阵，且有：r
(a1·a2
)
=r
(a1
)
∩r
(a2
)；n
(a
1·a2
)
=n
(a1
)
+n
(a2
)。
标签：矩阵
版权声明：文章由 知识问问 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.zhshwenwen.com/life/359572.html
