矩阵与矩阵的转置相乘

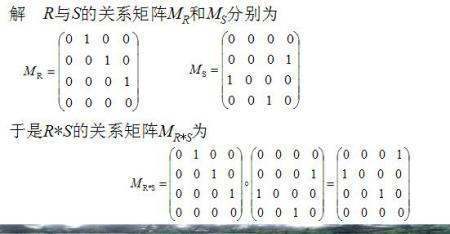
使用二维数组作为矩阵的存储结构，根据转置矩阵的特点，很容易得到转置矩阵。矩阵相乘的特点： （1）当矩阵A的列数等于矩阵B的行数时，A与B才可以相乘。 （2）乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。 （3）矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。两矩阵转置后相乘与相乘后转置不相等。证明如下：把矩阵A的行换成相应的列，得到的新矩阵称为A的转置矩阵，记作A^T或A’。根据基本性质(A±B)'=A'±B'；(A×B)'=B'×A'；(A')'=A；(λA')'=λA；det(A')=det(A)。所以转置后相乘和相乘后旅扰转置，也就是（A'核友×B'）和A'×B'一般是不相等的。必须是转置后相乘和相乘后转置两个之间的左右乘位置对调才相等；即（A'×B'）和B'×A'才是相等的。而B'×A'和A'×B'一般是不相等的，矩阵乘法一般不满足乘法交换律。扩展资料：矩阵转置的应用：如果AA^T=E（E为单位矩阵，A^T表示“矩阵A的转置矩阵”）或A^TA=E，则n阶实矩阵A称为正交矩阵。正交矩阵是实数特殊化的酉矩阵，因此总是正规矩阵。正交矩阵不一定是实矩阵。实正交矩阵（即该正交矩阵中所有元都是实数）可以改镇槐看做是一种特殊的酉矩阵，但是存在一种复正交矩阵，复正交矩阵不是酉矩阵。正交矩阵的一个重要性质就是它的转置矩阵就是它的逆矩阵。

标签：矩阵