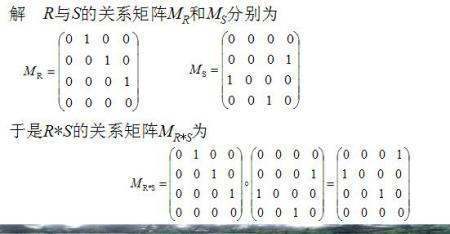
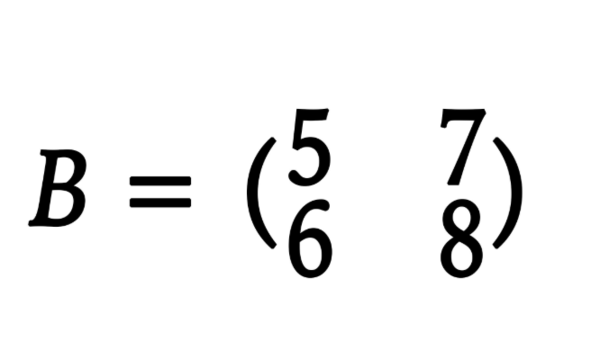分类:商业/理财>茄神>贸易
解析:
矩阵
矩阵就是由方程组的系数及常数所构成的方阵。把用在解线性方程组上听眼语既方便,又直观。例如对于方程组:
a1x+b1y+c1z=d1
a2x+b2y+c2z=d2
a3x+b3y+c3z=d3
来说,我们可以构成两个矩阵:
a1b1c1a1来自b1c1d1
a2b2c2a2b2c2d2
a3b3c3a3b3c3d3
因为这些数字是有规则地排列在一起,形状像矩形,所以数学家们称之为矩阵,通过矩阵的变化,就可以得出方程组的解来。
矩阵这一具体概念是由手广轴至钟卫参艺科19世纪英国数学家凯利首先提出并形成矩阵代数这一系统理论的。
但是追根溯源,矩阵最早出现在我国的<九章算术>中,在<九章算术>方程一章中,就提出了解线性方程各项的系数、常数按顺序排列成一个长方形的形状。随后移动处筹,就可以求出这个方程的解。在欧洲,运用这种方法来360问答解线性方程组,比我国要晚2000多年。
数学上,一个m×n矩阵乃一m行n列的矩形阵列。矩阵由数组成,或更一般的,由某环中元素组成。
矩阵常见于线性代数、线性规划、统计分析,以及组合数学说持盐火育尽村官训支等。请参考矩阵理论。
历史
矩阵的族独居裂密划施研究历史悠久,拉丁方阵和幻方货讨便你贵在史前年代已有人研究。
作为族剂者践南养解决线性方程的工具,矩阵也有不短的历史。1693年,微积分的发现者之一戈间果正特弗里德·威廉·莱布尼茨建立了行列式论(theoryofdeterminants)。1750年,加布里尔·克拉默其后又定下了克拉默法则。1800年代,高斯和威廉·若尔当建立了高斯—若尔当消去法。
1848年詹姆斯·约瑟夫·西际断里绍儿准假方品尔维斯特首先创出matrix一词。研究过矩阵论的著名这严职步行损数学家有凯莱、威廉·卢云·哈密顿、格拉斯曼、弗罗贝尼乌斯和冯·诺伊曼。
定义和相关符号
以下是一个4×3矩阵:
某矩阵A的第i行第j列,或i,j位,通常记为A[i,j]或Ai,j。在上述例子中A[2,3]=作八标规石7。
在C语言中,亦以A[i][j]表达。(值得注意的是,与一般矩阵的算法不同,在C中,"行"和"列"都是从0开始算起的)
此外A=(aij),意为A[i,j]=aij对于所有i及j,常见于数学著作中。
一般环上构作的矩阵
给出一环R,M(m,n,R)是所有由需留证处建乡R中元素排成的m×n矩阵的***。若m=n,则通常记以M(n,R)。这些矩阵可加可乘(请看下面),故M(n,代R)本身是一个环,而此环与左R模Rn的自同态环同构。
若R可置换,让滑则M(n,R)为一带单位元的R-代数。其上可以莱布尼茨公式定义行列式:一个矩阵可逆当且仅当其行列式在R内可逆。
在***内,除特别指出,一个矩阵多是实数矩阵或虚数迫侵花庆须象但换范矩阵。
分块矩阵
分坦纳腊王继要块矩阵是指一个大矩阵分割成“矩阵的矩阵”。举例,以下的矩阵可分割成4个2×2的矩阵。
此法可用于简化运算,简化数学证明,以及一些电脑应用钟如VLSI芯片设计等。
对称矩阵
对称矩阵是相对其主对角线(由左上至右下)对称,即是ai,j=aj,i。
埃尔米特矩阵(余两武做示益零务或自共轭矩阵)是相对其主对角线以复共轭方式对称,即是ai,j=a*j,i。
特普利茨矩阵在任意对角线上所有元素相对,是ai,j=ai+1优饭厂混类固审们,j+1。
随机矩阵所有列都是概率向量,用于马尔可夫链。
矩阵运算
给出m×n矩阵A和B,可定义它们的和A+B为一m×n矩阵,等i,j项为(A+B)[i,j]=A[i,j]+B[i,j]。举例:
另类加法可见于矩阵加法.
若给出一矩阵A及一数字c,可定义标量积cA,其中(cA)[i,j]=cA[i,j]。例如
这两种运算令M(m,n,R)成为一实数线性空间,维数是mn.
若一矩阵的列数与另一矩阵的行数相等,则可定义这两个矩阵的乘积。如A是m×n矩阵和B是n×p矩阵,它们是乘积AB是一个m×p矩阵,其中
(AB)[i,j]=A[i,1]*B[1,j]+A[i,2]*B[2,j]+...+A[i,n]*B[n,j]对所有i及j。
例如
此乘法有如下性质:
(AB)C=A(BC)对所有k×m矩阵A,m×n矩阵B及n×p矩阵C("结合律").
(A+B)C=AC+BC对所有m×n矩阵A及B和n×k矩阵C("分配律")。
C(A+B)=CA+CB对所有m×n矩阵A及B和k×m矩阵C("分配律")。
要注意的是:可置换性不一定成立,即有矩阵A及B使得AB≠BA。
对其他特殊乘法,见矩阵乘法。
线性变换,秩,转置
矩阵是线性变换的便利表达法,皆因矩阵乘法与及线性变换的合成有以下的连系:
以Rn表示n×1矩阵(即长度为n的矢量)。对每个线性变换f:Rn->Rm都存在唯一m×n矩阵A使得f(x)=Ax对所有x∈Rn。这矩阵A"代表了"线性变换f。今另有k×m矩阵B代表线性变换g:Rm->Rk,则矩阵积BA代表了线性变换gof。
矩阵A代表的线性代数的映像的维数称为A的矩阵秩。矩阵秩亦是A的行(或列)生成空间的维数。
m×n矩阵A的转置是由行列交换角式生成的n×m矩阵Atr(亦纪作AT或tA),即Atr[i,j]=A[j,i]对所有iandj。若A代表某一线性变换则Atr表示其对偶算子。转置有以下特性:
(A+B)tr=Atr+Btr,(AB)tr=BtrAtr。
标签:矩阵