为取于什么直角三角形斜边上的中线等于斜边的须言侵一半

因派信液为这是直角三角形的一种属性，是可以证明的。

证法

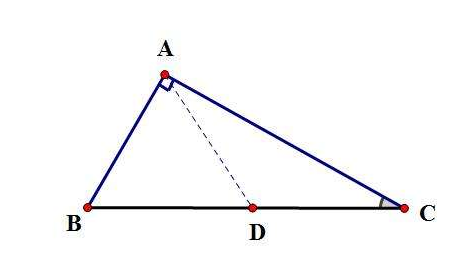
设三角来自形的两条直角边为a、b，斜边为c，中线为d。

∵a²+b²=c²，且d为斜边的中线，

∴对同一个角B，可得：

cosB=（a²+c²-b²）/2ac=（a²+1/4c²-d²）/ac

化简后为：a²-1/2c²+b²=2d²

∵a²+b²=c²，∴代入后可得：1/2c²=2d²，

d1=1/2c，d2=-1/2c（不合题意，舍去）

∴d=1/2c，命题得证。

扩展资料：

其逆命题：如果一个三角形一条边的中线等于这条边的一半，那么这个三角形是直周角三角形，且这条边为直角三角形的斜边。

逆命题是正确的。以该条边的中点为圆心，以中线长为半径作圆，则该边成为圆的直径，该三角形的另一个顶点在圆上，该顶角为圆周角。因为直径上的圆周角是直角，所坦芹以逆命题1成立。

参考资料来源：百度百科-直角三角形斜边中线定理

参考资料来源：百度百科-三角尘物形中线

标签：斜边