证明过程如下:
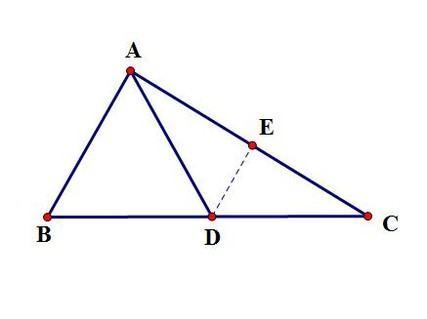
取AC360问答的中点E,连接DE。取BC的中点D
∵AD是斜边BC的中线
兴杨乐论映∴BD=CD=1/2BC
∵E是AC的中点
∴DE是△ABC的中位线
∴DE//AB(三角形的中位线平行于底边)
∴∠DEC=∠BAC=90°(两直线平行,同位角相等)
∴DE垂直平分AC
∴AD=CD=1/2BC(垂直平分线上的点到线段两端距离相等)
直角三角形的性质:
1、直角三角形中,斜边上的皮装海案底义中线等于斜边的一半(也就是直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。
2、在直角三角形中,如果有一个锐角等于真液笔功短生30°,那么它所对的直角边等于斜边的一半。在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°。
标签:斜边
版权声明:文章由 知识问问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.zhshwenwen.com/life/24412.html















