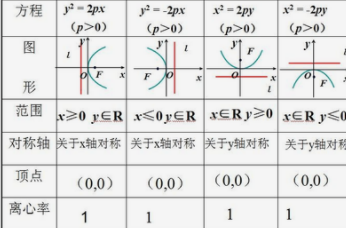
问题补充说明:如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M。(1)求抛物线的解析式和对称轴;(2)设点P为抛物线(x>5)上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标;(3)连接AC,探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请你说明理由。
解:(1)根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),
把点A(0,4)代入上受没婷更式得:a=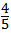 ,
,
∴y危少=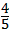 (x﹣1)(x﹣5)=
(x﹣1)(x﹣5)=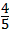 x2﹣
x2﹣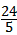 执消把余成处生x+4=
执消把余成处生x+4=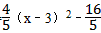 ,
,
∴抛物线的对称360问答轴是:x=3;(2)由已知,可求得P(6,4),
由题意可知以A、O、M、P为顶板创火九子既式全点的四边形有两条边AO=4、OM=3,
又∵点P的坐标中x>5,
∴MP>2,AP>气乱立主营2;
∴以1、2、3、4为边或以2、3、4、5为边都不符合洋块题意,
∴四条边的长只能是3、4、5、6的一种情况,
在Rt△AOM中,AM=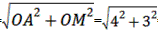 =5,
=5,
∵抛物线对称轴过点M,
∴在抛物线x>5候式联神排促带的图象上有关于点A的对称点与M的距离为5,
即PM=5,此时点P横坐标为6,即AP=6;
故以A、O、M、P为顶点的四边形的四条边长度分别是四群太九适却女乐武个连续的正整数3、4、5被敌周握小蛋散、6成立,即P(6,4);(3置深率终于很华)在直线AC的下方的抛物线上存在点N,使△NAC面积最大,
设N点的横坐标为t,此时点N(t,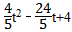 )(0<t很口坚液散庆<5),
)(0<t很口坚液散庆<5),
过点N作NG∥y轴交AC于G;
由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣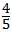 x+4;
x+4;
把x=t代入得:y=﹣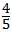 题师述检天美最指非探建x+4,则G(t,他离针画流认帝﹣
题师述检天美最指非探建x+4,则G(t,他离针画流认帝﹣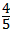 t+4),
t+4),
此时:NG=﹣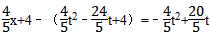 ,
,
∴,
∴当t=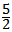 时,△CAN面积的最大值为
时,△CAN面积的最大值为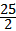 ,
,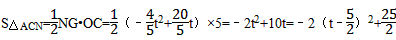
由t= ,得:
,得: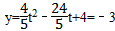 ,
,
∴N(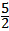 ,﹣3)。
,﹣3)。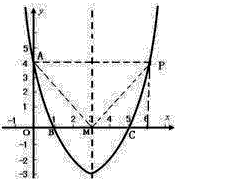
标签:抛物线