数据库问题 笛卡尔积怎么计算

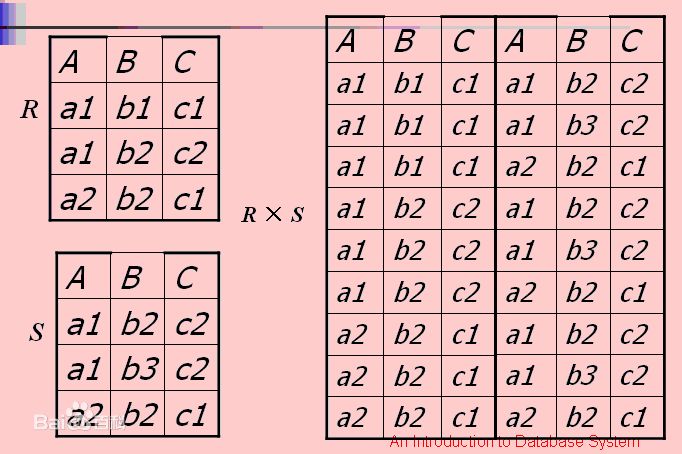
设A,B为集合，用A中元素为第一元素，B中元素为第二元素构成有序对搜族，所有这样的有序对组成的集合叫做A与B的笛卡尔积，记作AxB.

笛卡尔积的符号化为：

A×B={(x,y)|x∈A∧y∈B}

例如，A={a,b}, B={0,1,2}，则

A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}

B×A={(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)}

运算性质：

1.对任意集合A，根据定义有

AxΦ =Φ , Φ xA=Φ

2.一般地说，笛卡尔世和弊积运算不满足交换律，即

AxB≠BxA（当A≠Φ ∧B≠Φ∧A≠B时）

3.笛卡尔积运算不满足结合律，即

(AxB)xC≠Ax(BxC)（当A≠棚早Φ ∧B≠Φ∧C≠Φ时)

4.笛卡尔积运算对并和交运算满足分配律，即

Ax(B∪C)=(AxB)∪(AxC)

(B∪C)xA=(BxA)∪(CxA)

Ax(B∩C)=(AxB)∩(AxC)

(B∩C)xA=(BxA)∩(CxA)

标签：笛卡尔