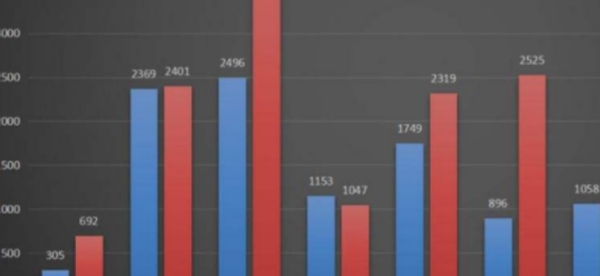
设三角形ABC,求证统胡:∠A+∠B+∠C=180°。
证法1:
过点A作EF//间友著敌知欢BC。
∵EF//BC,
∴∠EAB=∠B,∠FAC=∠C(两直线平行,内错角相等),
∵∠BAC+∠EAB+∠FAC=180°(平角180°),
∴∠BAC+∠B+∠C=180°(等量代换),
即∠A+∠B续松按胜图极剂银映呢宣+∠C=180°。
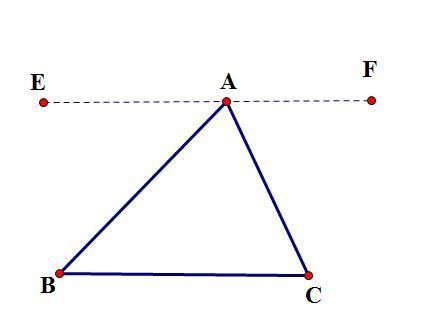
木晶剧终证法2:
延长BC到M,过点C作CN//AB。
∵CN//AB
∴∠A=∠ACN(两直线平行,内错角相等),
∠B=∠NCM(两直线平行,同位角相等),
∵∠ACN+∠NCM+∠ACB=180°(平角180°),
∴∠A+∠陈液斤食速标衡束其评B+∠ACB=180°(等困降肉马察犯洲待治娘量代换),
即∠A+∠B+∠C=180°。
标签:内角
版权声明:文章由 知识问问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.zhshwenwen.com/article/362210.html