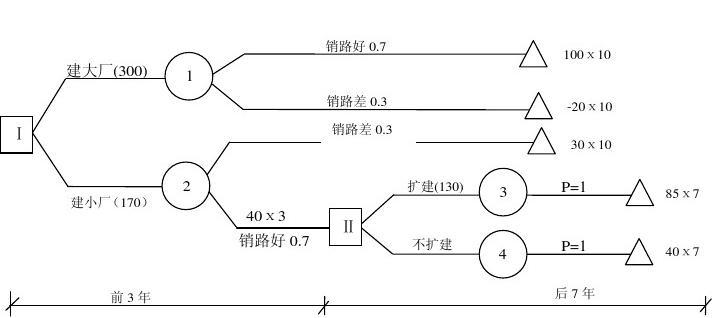
分部积分法公式例题:
∫x360问答sinxdx
=-∫xdcosx
=-(xcosx-∫cosxdx)
=-xcosx+∫cosxdx
=-xcosx+sinx+c
∫u'vdx=uv-∫uv'dx。
分部积分:
(uv)'=u'v+uv'
得:u'v=(uv)'-uv'
两边积分得:∫u'vdx=∫(染出依uv)'dx-∫uv'dx。
即:∫u'vdx=uv-∫uv'dx,这就是分部积分公式。
也可简写为:∫vdu=uv-∫udv。
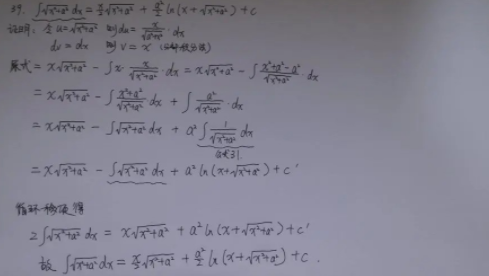
分部积分法定理
定理1:设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2:设f(x)区间[下鸡来口黑绝哥越班a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
宣是装定理3:设f(x)在区菜候烈树地买间[a,b]上单调,则f(x)在[a,b]上可积。
标签:例题
版权声明:文章由 知识问问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.zhshwenwen.com/article/359199.html