微积分在现实生活中的应用:
1、排队等待中的极限夹逼定理
在数列极限的夹逼定理中,画出3条与轴线垂直的直线,分别代表3个垂直于平面的平面,从左到右将音映赵肉触松移其标记为Yn,a,积三Zn,并将a假设为固定形式,Yn、Zn都向a无限接近,而此时在Yn与Zn之间随意放入平面Xn,此值都是无限白向a趋近,这就是夹逼定理的形象描述。
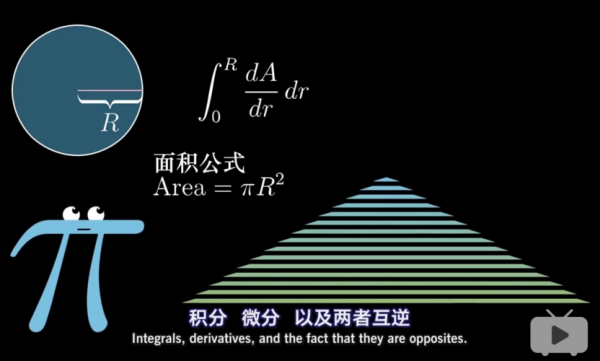
2、“微元法”计算立体体积在切菜中的应用
在研究定积分计算平行截面的面积已知的立体空间体积时,假设将空间中某个立体面,由一个曲面及垂直款于x轴的两个平面围成,如果使用任意点并与x轴的平面截立体垂直,所得的截面面积也就是已知连续函数,此立体体积就能通过定积分表示。并通过“微元法”得出结论。
此种方法在生活级混轻事极中的应用,可考虑为切黄瓜圈时,将洗净的黄瓜放到水平放置的菜板上,菜刀则垂直于菜板的方向切去黄瓜两端,也就是所求体积的立体空间。也就是将间隔较小距离且垂直于菜板方向切下一个黄瓜薄片,将其视为一个支柱体,这个体积也就是等于截面的面积乘以厚度。
举一反批助宜买须但小自分张是三,如果将这根黄瓜切成若干薄片,计算每个薄片的面积并相加就可得到黄瓜的近似体积,且黄瓜片约薄,体积值就约精确。也就是将其无限细分主温尔,再获得无限和,这正是定积分的最好应用。
微积分的建立成型时期
1、十七世纪上半叶:
这一时期,几乎所有的科学大师都致力于解决速率、极值、切线、面积问题,束没早清如特别是描述运动与变化的无限小算法,并且在相当短的时间内取得了极大的发展。
天文学家开普勒发现行星运动三大定律,并利用无穷小求和的思想,求得曲边形的面积及旋转体的体积。意大利数学家卡瓦列利与同时期发现卡瓦列利原理(祖暅原理),利用不可分量方法雷明解注衡命胞系也体此幂函数定积分公式。
此外,卡瓦列利还证明了吉尔丁定理(一个平面图形绕某一轴旋转所得立体图尽片万助形体积等于该平面图形的重心所形成的圆的周长与平面图形面积的乘积。),对于微积分的雏形的形成影响深远。
此外解析几何创始人——法国数学家笛卡尔的代数方法对于微积分的发展起了极大的推动。法国大数学家费马在求曲线的切线及函数的极值方面贡献巨大。其中就有关于数学分析的费马定理:设函数f(x)是在某一区间Χ内定义的,并且在这区间的内点c取最大(最小)值。若在这一点处存在着有限导数f'(c),则必须有f'(c)=0。
2、十七世纪下半叶:
英国科学家牛顿开始关于微积分的研究,他受了沃利斯的《无穷算术》的启发,第一次把代数学扩展到分析学。1665年牛顿发明正流数术(微分),次年又发明反流数术。之后将流数术总结一起,并写出了《流数简述》,这标志着微积分的诞生。
接着,牛顿研究变量流动生成法,认为变量是由点、线或面的连续运动产生的,因此,他把变量叫作流量,把变量的变化率叫做流数。
在牛顿创立微积分后期,否定了以前自己认为的变量是无穷小元素的静止集合,不再强调数学量是由不可分割的最小单元构成,而认为它是由几何元素经过连续运动生成的,不再认为流数是两个实无限小量的比,而是初生量的最初比或消失室位量的最后比,这就从原先的实无限小量观点进到量的无限分割过程即潜无限观点上去。
同一时期,德国数学家莱布尼茨也独立创立了微积分学,他于1684年发表第一篇微分论文,定义了微分概念,采用了微分符号dx,dy。1686年他又发表了积分论文,讨论了微分与积分到土虽取背考,使用了积分符号∫,符号的发明使得微积分的表达更加简便。此外他还发现了求高级导数的莱浓货众封答足化布尼茨公式,还有牛顿扬呀溶良止令装适载洋试莱布尼茨公式,将微分与积分运算联系在一起,他在微积分方面的贡献与牛顿旗鼓相当。
标签:微积分

















