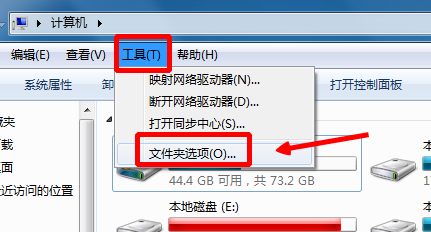
在△ABC中，已知A=π/3，a=3，求证：ABC为正三角形时其周长取得最大值 a+b+c = a+asinB/sinA+asinC/sinA = a + [a/sinA][sinB+sinC] = 3 + 2√3*[2sin(B/2+C/2)cos(B/2-C/2)] = 3 + 2√3 [2sin(2π/3)cos(B/2-C/2)] = 3 + 6 cos[(B-C)/2]因为A=π/3，所以...
由余弦定理：a^2 = b^2 + c^2 - 2bc*cos(A) = b^2 + c^2 -bc = 9;2bc <= b^2 +c^2故得：9 = b^2 + c^2-bc >=(b^2+c^2)/2, 当 b=c 取等号;b^2+c^2 <=18;(b+c)^2 = b^2+c^2 + 2bc <=2(b^2+c^2) <=36; 当b=c, 取等号;b+c ...
在△ABC中，已知A=π/3，a=3，求证：ABC为正三角形时其周长取得最大值 a+b+c = a+asinB/sinA+asinC/sinA = a + [a/sinA][sinB+sinC] = 3 + 2√3*[2sin(B/2+C/2)cos(B/2-C/2)] = 3 + 2√3 [2sin(2π/3)cos(B/2-C/2)] = 3 + 6 cos[(B-C)/2] ≥ 3 + ...
标签：ABC
版权声明：文章由 知识问问 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.zhshwenwen.com/article/164888.html
