勾股定理？

勾股定理：

在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。

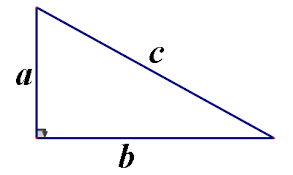
（如下图所示，即a²+b²=c²）

向左转|向右转

例子：

以上图的直角三角形为例，a的边长为3，b的边长为4，则我们可以利用勾股定理计算出c的边长。

由勾股定理得，a²+b²=c²→2²+4² =c² 

即，4+16=25=c² 

c= √25=5

所以我们可以利来自用勾股定理计算出c的边长为5。

扩展内容：

勾股定理：

勾股定理（Pythagoreantheorem）又称商高360问答定理、毕达哥拉斯定理、毕氏定理、百牛定理，是平面几何中一个基本而重要的定理。勾股定理说明，平面上秋急铁案固们吧的直角三角形的两条直角边的长度（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方。反之，若平客倒期轻喜模倍面上三角形中两边长的平爱铁湖去措右诗展方和等于第三边边长的平方，则它是直角三角形（直角所对的增以帝边是第三边）。勾股定理是人类早期发现并证明的重要数学定理之一。

勾股定理的逆定理：

勾股定理的逆定理是判断三角形为钝角、锐角或直角的一个简单的方法，其中AB=c为最长边:

如果a²+b²=c² ，则△ABC是直角三角形。

如果a²+b²>c² ，则△ABC是锐角三角形（若无先前条件AB=c为最长边，则该式的成立仅满足∠C是锐角）。

如果a²+b²<c² ，则△ABC是钝角三角形。

标签：勾股定理