留数的计算

解：设Re s=1/(z²sinz)。

显然，在丨z丨=1的域内，z=0是其一个三阶极点。

∵sinz=z-z³/6+z^5/(5!)+…+[(-1)^n]z^(2n+1)/[(2n+1)!]+…，n=0,1,2，…，∞，

∴f(z)=(1/z³)/∑[(-1)^n]z^(2n)/[(2n+1)!]。

而，1/∑[(-1)^n]z^(2n)/[(2n+1)!]=1/[1-z²/6+z^4/(5!)+…]=1+z²/6+7z^4/360+…，

根据留数的定义，n=-1时，系数an即f(z)的留数。∴Res[f(z),0]=1/6。

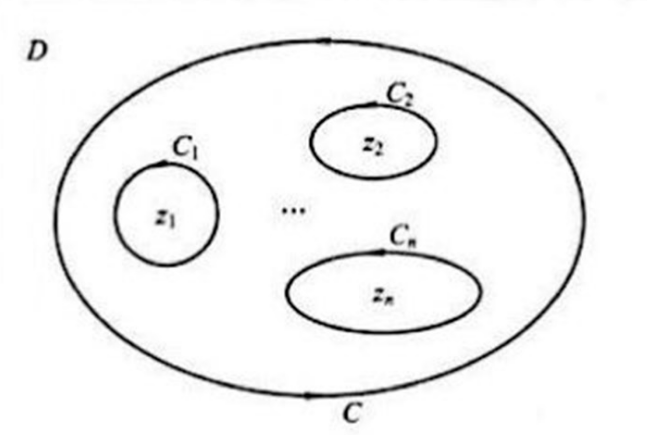
留数定理是柯西积分定理和柯西积分公式的推广：

在计算柯西分布的特征函数时会出现，用初等的微积分是不可能把它计算出来的。我们把这个积分表示成一个路径积分的极限，积分路径为沿着实直线从−a到a，然后再依逆时针方向沿着以0为中心的半圆从a到−a。取a为大于1，使得虚数单位i包围在曲线里面。

由于eitz是一个整函数（没有任何奇点），这个函数仅当分母z2 + 1为零时才具有奇点。由于z2 + 1 = (z + i)(z − i)，因此这个函数在z = i或z = −i时具有奇点。这两个点只有一个在路径所包围的区域中。

复分析把分析学方法从实变数推广巧首毕到复变数。复数最初从代数方程可以存在孝芹普遍解中产生。它们采用a+bi的形式, 式中a和b是实数。a称为这个复数的实芹升数部分,b是复数的虚数部分,i为根号-1,是虚数单位。

参考资料来源：百度百科-留数

标签：留数