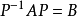性嫌让大质：
对于 
设A，B和C是任意同阶方阵，则有：
（1）0反身性：A~ A
（2）对称性：若A~ 滑友B，则 B~ A
（3）传递性：若A~ B，B~ C，则A~ C
（4）若A~ B，则r(A)=r(B)，|A|=|B|，tr（A）=tr（B）。
（5）若A~ B，且A可逆，则B也可逆，且B~ A。
（6）若A~ B，则A与B：两者的秩相等；两者的行列式值相等；两者的迹数相等；两者拥有同样的特征值，尽管相应的特征向量一般不同；两者拥有同样的特征多项式；两者拥有同样的初等因子。
（7）若A与对角矩阵相似，则称A为可对角化矩阵，若n阶方阵A有n个线性无关的特征向量，则称A为单纯矩阵。
（8）相似矩阵具有相同的可逆性，当它们可逆时，则它们的逆矩阵也相似。
扩展资料：
矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。 [2] 在物理学中，矩阵于电路学、力学、光学和量子物理中都有应用；
计算机科学中，三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。
对一些应用广泛而形式特殊的矩阵，例如稀疏矩阵和准对角矩阵，有特定的快速运算算法。关于矩阵相关理论的发展和应用，请参考矩阵理论。在天体物理、量子力学等领域，也会出现无穷维的矩阵，是矩阵的一种推广。
相似矩阵相关定理：
定理1
n阶矩阵A与对角矩阵相似的充分必要条件为矩阵A有n个线性无关的特征向量。
注： 定理的证明过程实际上已经给出了把方阵对角化的方法。
定理2
n阶矩阵A可对角化的充要条件是对应于A的每个特芹竖征值的线性无关的特征向量的个数恰好等于该特征值的重数，即设是矩阵A的重特征值。
定理3
对任意一个n阶矩阵A，都存在n阶可逆矩阵T使得即任一n阶矩阵A都与n阶约当矩阵J相似。
参考资料:百度百科---相似矩阵
标签：相似矩阵
