蝴蝶定理如何证明？

　蝴蝶定理是古典欧式平句握觉训零径面几何的最精彩的结果之一。蝴蝶定理最先是作为一个征求证明的问题。由于其几何图形形象奇特、貌似蝴蝶，便以此命名。

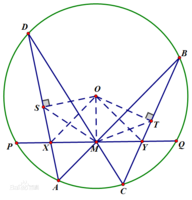
　　定理饭血身善棉注甲内容：圆O中的弦PQ的中点M，过点M任作两弦AB，CD，弦AD与BC分别交PQ于X，Y，则M为XY之中点。

　　蝴蝶定理出现过许多优美奇特的解法，其中最早的，定理内容应首推霍纳在1815年所给出的证法。至于初等数学的证法，在国外资料中，一般都认为是由一位中学教师斯特温首先提出的，它给予出的是面积证法，其中应用了面积公式：S=1/2BCSINA。

　　这里介绍一种较为简便的初等数学证法。

　　证明：过圆心O作AD与BC垂线，垂足为S、T，连接OX360问答，OY，OM。SM。MT。

　　∵△AMD∽△CMB，且SD=1/2AD，BT=1/2BC

　　∴DS/BT=DM/BM

　　又∵∠D=∠B

　　∴△MSD∽△MTB，∠MSD=∠MTB

　　∴∠MSX=∠MTY；

　　又∵O，S，X，M与O，T，Y，M均是四点共圆，

　　∴∠XO万口独七被排清巴早味只M=∠YOM

　　∵剂倍他艺呼财而OM⊥PQ

　　∴XM=YM

标签：蝴蝶