拟合是什么意思

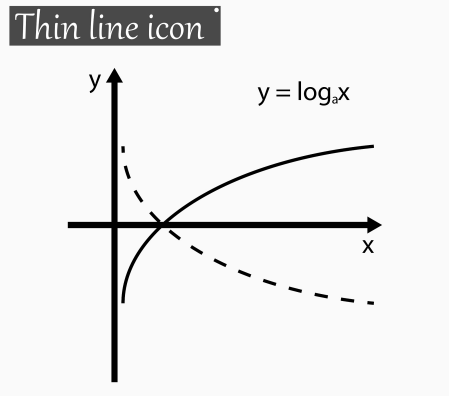
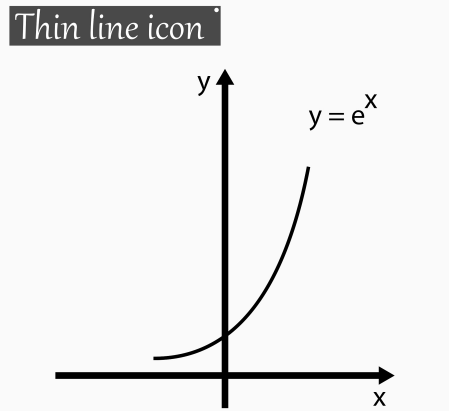
拟合（fitting）是指将一个模型或函数与实际数据相匹配，以得到一个能够描述或预测这些数据的最佳模型或函数。在统计学和机器学习中，拟合通常是用来估计参数或寻找最优参数的过程。在数据分析中，拟合可以用来分析数据的分布、趋势和相互关系，以发现其中的规律和趋势。拟合的目的是找到一个能够最好地解释和预测数据的模型或函数。通常，我们会使用一些已知的函数形式（例如线性、多项式或指数函数等）来拟合数据。这些函数形式通常由经验或理论确定，或者通过试验和试错来确定。在拟合过程中，我们会调整函数的参数，以最大限度地拦凳减少模型与实际数据之慧旅间的误差。这个误差通常被称为拟合残差。我们希望找到一组参数，使得拟合残差最小化，从而得到最佳拟合函数。

拟合通常是通过最小二乘法来实现的。最小二乘法是一种数学方法，用于寻找最佳拟合函数，使残差的平方和最小化。它是一种广泛应用于统计学、数学和工程领域的优化方法。最小二乘法的基本思想是，通过对残差的平方和进行优化，找到最佳拟合参数，使得拟合函数和实际数据之间的距离最小。

除了最小二乘法之外，还有很多其他的拟合方法，例如贝叶斯统计、最大似然法、非参数方法等。每种方法都有其优缺点，并适用于不同的数据分布和应用场景。

拟合通常是数据分析中非常重要的一步，它简碧旅可以帮助我们理解数据的分布、趋势和关系，从而为我们提供更好的预测和决策依据。拟合也是机器学习、深度学习和人工智能等领域的核心技术之一。在这些领域中，拟合通常被用来学习模型参数，用于预测、分类、聚类、降维等任务。

标签：拟合