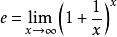e的负ln2次方等于多少

（e）^-ln2=(e^ln2)^-1=2^-1=1/2。

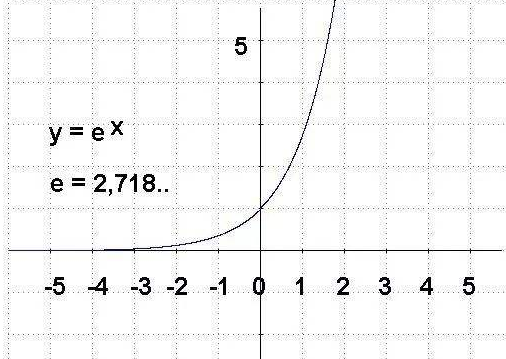
e，作为数学常数，是自然对数函数的底数。携陆有时称它为欧拉数（Euler number），以瑞士数学家欧拉命名；也有个较鲜见的名字纳皮尔常数，以纪念苏格闭隐扰兰数学家约翰·纳皮尔 (John Napier)引进对数。它就像圆周率π和虚数单位i，e是数学中最重要的常数之一。

定义：

其数值约为（小数点后100位）：“e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274”。

扩展资料

1、随着利息、对数、指数的发明，人们发现了e的存在。

2、1元存1年，在年利率100%下，无穷次的利滚利就会达到e。

3、e和π一样都是内在规律，反映了指数增长的自然属性。

4、大自然中到处都有对数螺线的身影。

5、其他底数都是发明出来方便人使用，只有e为底数是被发现的。

6、数学家发现以e为底数的对数轿旦是计算中最简、最美、最自然的形式，把e冠以自然底数、自然常数之名，把e为底数的对数称为自然对数，是数学家们用自己的方式对e所进行的美学评价。

标签：ln2