正态分布可加性是X+Y~N(3,8)。
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由棣莫弗(Abraham de Moivre)在求二项分布的渐坦尘近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
扩展资料:
图形特征
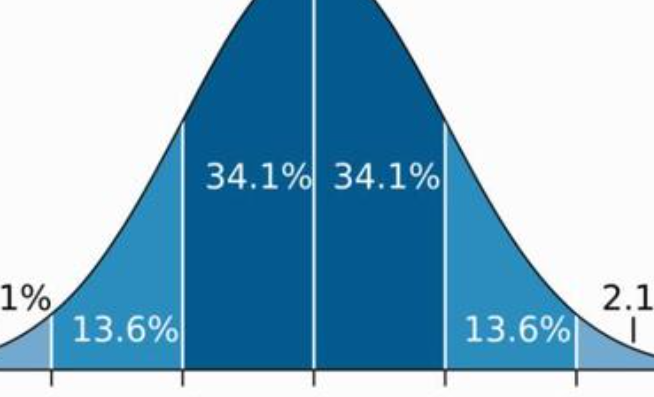
集中性:正态曲线的高峰位于正中央,即均数所在的位置。
对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交。
均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。
曲线贺漏与横轴间的面积总等于1,相当于概率密度函数的函数从正无穷到负无禅信烂穷积分的概率为1。即频率的总和为100%。
标签:可加性
版权声明:文章由 知识问问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.zhshwenwen.com/article/47894.html