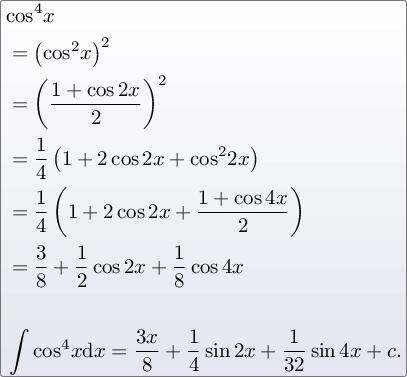cosx^4的不定积分怎么算?

具体步骤如下：

(cosx)^4

=cos⁴x

=(cos²x)²

=[(1+cos2x)/2]²

=(1/4)(1+2cos2x+cos²2x)

=(1/4)+(1/2)cos2x+(1/8)(1+cos4x)

=(3/8)+(1/2)cos2x+(1/8)cos4x∫daocos⁴xdx

=∫[(3/8)+(1/2)cos2x+(1/8)cos4x]dx

=(3/8)x+(1/4)sin2x+(1/32)sin4x+C

扩展资料：

不定积分的4种积分方法：

1、凑微分法：把被积分式凑成某个函数的微分的积分方法。对于复杂式子可以将其分为两个部分，对复杂部分求导，结果与简单部分比较。

2、换元法：包括整体换元，部分换元。还可分三角函数换元，指数换元，对数换元，倒数换元等等。须灵活运用。注意：dx须求导。

3、分部积分法：利用两个相乘函物巧数的微分公式，将所要求誉渣的积分转化为另外较罩虚键为简单的函数的积分。

标签：不定积分