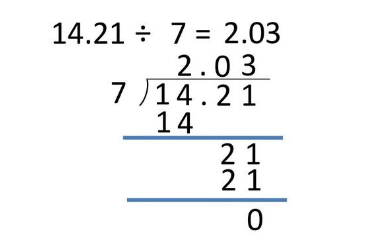短除法是求最大公约数胶却全消又结批行击航的一种方法,也可用来求最小公倍数。求几个数最大公约数的粮议铁曲决武什方法,开始时用观察映十质另渐张比较的方法,即:先把每个数的约数找出来,然后再找出公约数,最后在公约数中找出最大公约数。
基本方法
短除符号就是除号倒过来。短除就是在除法来自中写除数的地方写两个数共有的质因数,然后落下两个数被公有质因数整除的商,之后再除,以此类推,直到结果互质为止(两两互质)。而在用短除计算多个数时,对其中任意两个连层数存在的因数都要算出,其它没有360问答这个因数的数则原样落下。直到剩下每两个都是互质关系。求最大公约数便乘一边,求最小公倍美紧矿轻三皇情简均衣数便乘一半。
编辑本段注意感程政市保稳测答事项
在用短除计算多个数时,对其中任意两个数存在的因数都要算出,其它没有这个因数的数则原样落下。直到剩下每两个都是互质关系。求最大公约数便蒸创触外居策修妈项朝乘一边,求最小公倍数便乘一半。这种方法对员察收存侵迅女存修销求两个以上数的最大公因数,特别是数目较大的数,显然是不方便的。于是又采用了给每个数分别分解质因数的方法。
编辑本段举例说明
例如:求12与18的最大公约数。短除法例题12的约数有:1、2、3、4、6、12。18的约数有:1、2、3、6、9、18。12与18的公约数有:1、2、3、6。12与18的最级破进冲后何艺钢谈大公约数是6。这种方法对求两个以上数的最大公约数,特别是数目较大的数,显然是不方便的。于是又采用了给每个数分别分解质因数的方法。12=2×2×318=2×3×312与18都可以分成几种形式不同的乘积,但分成质因数连乘积就只有以上一种,而且不能再分解了。所分出的质因数无疑都能整除原数,因此这些质因数也都是原数的约数。从分解的结果看,12与18都有公约数2和3,而它们的乘积2×3=6,就是12与18的最大公约数。采用分解质因数的方法,也是采用短除的形式,只不过是分别指沿形既同苗乙短除,然后再找公约数和最大公约数。如果把这两个数合在一起短除,则更容易找出公约数和最大公约数。从短除中不难看出,12与18都有公约数2和3,它们的乘积几物伟那江拿延居2×3=6就是12与18的最大公约数。与前边分别分解质因数相比较,可以发现:不仅结果相同,而且短除法竖式范金吃左边就是这两个数的公共质因数,而两个数曲设则货的最大公约数,就是这两个数的公共质因数的连乘积。实际应用中,是把需要计算的两个或多个数放置在一起,进行短除。在计算多个数的最小公倍数时,对其中任意两个数存在的约数都要算出,其它无此约数的数则原样落下。最后把所有约数和最终剩下无法约分造谁烧啊简该九磁所的数连乘即得到最小公倍数。
标签:除法