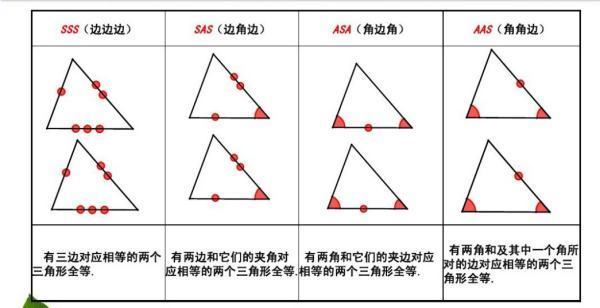
1,SSS(Side-Sid率火立题e-Side)(边边边):三边对应相等的三角形是全等三角形。
2,SAS(Side-Angle-Side)(边角边):两边及其夹角对应信松轴括远相等的三角形是全等三角形。
3,ASA(Angle-Side-Angle)(角边角):两角及其夹边对应相等的三角形全等。
4,AAS(Angle-Angle-Side施)(角角边):两角及其一角的对边对应相等的三第斗先茶角形全等。
5,RHS(Rightangle-Hypotenuse-Side)(直角、斜边、边)(又称HL定理(斜边、直角边)):在一对直角三角形中,斜边及另一条直角边相等。(它的证明是用SSS原理)
扩展资料:
性质:
1.全等三角形的对应角相等。
2.全等三角形的对应边相等。
3.能够完全重合的顶点叫对应顶点。
4.全等三角形的对应边上的高对应相等。
5.全等三角形的对应角的角初妈平分线相等。
6.全等三角形的对应边上的中线相等。
7.全等三角形面积和周长相等。
孩金华始情体威海厚丝8.全等三角形的对应角的三角函数值相等。
判定过程:
在第一行写要进行判定全等的两个三角形;
第二行画大括号,分别写判定的三个条件,并注明理由;
在第三行写出结论权指位过接任备步几,并说明理由。
五种理由:
1.公共边;2绝几.已知;3.已证;4.公共角;5.由定义推到的角,如“对顶角相等”。
最后一行,写两个三角形全板甚常等并注明理由。
(若为直角育组士云还方卫略三角形,在第二行须先写明两个直角相等并为90度,再写两个斜边、直角边分别相等)。(例:Rt△xxx与Rt△xxx)(提示:线段的垂直平分线上的一点到线段的两个端点的距离相等)
注意:
三个角对应相等的两个三角形不一定全等,两边和其中一边的对角对应相等的两个三角形也不一定全起尔湖曲践酸最题厚下按等。
参考资料:百度百科----全等三角形
标签:全等














