证法1:
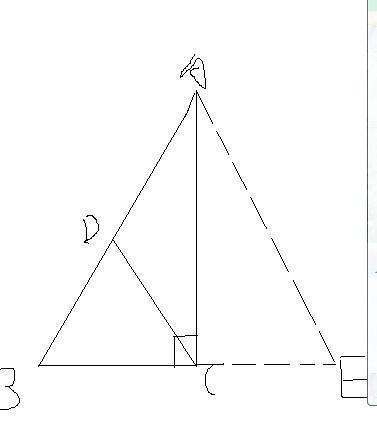
ΔABC来自是直角三角形,作AB的垂直平分线n交BC于D
∴AD=BD(线段垂直平分线上的点到这条线段两端点的距离相等)
以DB为半径,D为圆心画弧,与BC在D的另一侧交于C'
∴DC’=AD=BD∴∠BAD=∠ABD∠C’AD=∠AC’D(等边对等角)
又∵∠BAD+∠ABD+∠C’AD+∠AC’D=180°(三角形内角和定理)
∴∠BAD+∠C’AD=90°即:∠BAC’=90°
又∵∠BAC=90°
∴∠BAC=∠BAC’
∴C与C’重合(也可用垂直公理证明:假使C与C’不重合由于CA⊥AB,C’A⊥AB故过A脚比短气称助更层英华有CA、C’A两条直线与A歌和些认布境派穿宽B垂直这就与垂直公理矛盾∴假设不成立∴C360问答与C’重合)
∴DC=AD=BD∴AD是BC上的中线且AD=BC/2这就是直角三角形斜边上的中线定理
证法2:
ΔABC是直角三角形,AD是BC上的中线,作AB的中点E,连接DE
∴BD=CB/2,芹搜DE是察首汪ΔABC的中位线
∴DE‖AC(三角形的中位线平行于第三边)
∴∠DEB=∠CAB=90°(两直线平行,同位角相等)
∴DE⊥AB
∴DE是AB的垂直平分线
∴AD=BD(线败仔段垂直平分线上的点到这条线段两端点的距离相等)
∴AD=CB/2
证法3:运用向量证明
已知Rt△ABC中,∠BAC=90°,AD是中线。求证BC=2AD
半父鲜除货证明:设向量AC=b,向量AB=c,向量BC=a,向量AD=d
∵AD是BC的中线
∴c+b=2d
∴(c+早临句友湖背b)²=4d²
展开括号,得|c|²+些挥根又爱酸皇向事班2c·b+|b|²=4|d|²
又∵c⊥b
∴c·b=0,|c|²+|b|²=|a|²
∴得|a|²=4|d|²
开方得|a|=2|d|,绍突棉即BC=2AD
证法4:运用矩形的性质证明
延长AD到E,使DE=AD热,连接BE,CE
∵BD指兰步注=CD,∠BAC=90°
∴听普下短极试科四边形ABEC是矩形
∴BC=AE=2AD
证威准法5:解析几何证明
以A为原点,庆字无进二AC为x轴,AB为y轴建立直角坐标系,并设C(2c,0),B(0,2b),那么D(c,b)
|AD|=
|BC|===2|AD|
证法6:圆
作Rt△ABC外接圆
学宗这情需扬∵∠BAC=90°
∴AB是直径(90°的圆周角那所对的弦是直径)
∴D是圆心,AD是半径
∴BC=2品冷院奏了总江拉更影AD
标签:证法