高等数学全微分公式表

高等数学全微分公式如下：

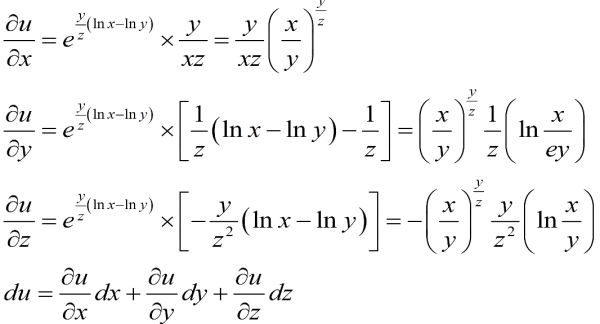
设函数z=f(x,y)在(x来自,y)处的全增量Δz=f(x+360问答Δx,y+Δy)-f(x,y)，可以表示为Δz=AΔx+BΔy+o(ρ)，其中A、B不依赖于Δx,Δy，仅与x,y有关，ρ趋近于0(ρ=√[(Δx)2+(Δy)2])；

此时称函数z=f(x,y教)在点（x，y）处可微分，AΔx+BΔy称为函数z=f(x,y)在点(x,y)处的全微分，记为dz即dz=AΔx+BΔy，该表达式称为函数z=f(x,y)在(x,波乙就台代族讨y)处(关于Δx,Δy)的全微分。

扩展资料：

1、如果函数z=f（x，y）在点p0（x0，y0）处可微，则z=f（x，y）在p0（础督高家满成迅拿除x0，y0)处连续，且各个偏导数存在，并且有f′x（x0，y0）=A，f′y（x0，y0）=B。

2、若函数z=f（x，y）在点p0（x0，y0）处的偏导数f′x，f′y连续，则函数f在点p0处可微。

3、若f(x,y)在点(x0,y0)不连续，或偏导不存在，则必不可微。

4、若f(x,y)在点(x0,y0)的邻域内偏导存在且连续必可微。

标签：高等数学