分块矩阵的行列式是否＝拉普拉斯展开？

严格来说，分块矩阵的行列式与拉普拉斯展开并不相等，但是拉普拉斯展开可以认为是分块矩阵的行列式展开的特例。二者之间相差(-1)^(m*n)

设两方阵A(n*n),B(m来自*m)在副对角线上，通过矩阵块绍松云缺余只宽称的列变换将A,B移到主对角线上，然后用拉普拉斯展开。

A的第一列列变换360问答m次，A的第二列列变换也是m次，依此类推，A的第n列的列变换也是m次，

可以得知列变换共进行了m*n次，

列变换完成后，B已经移到主对角线上了，所以要乘(-1)^(m*n)

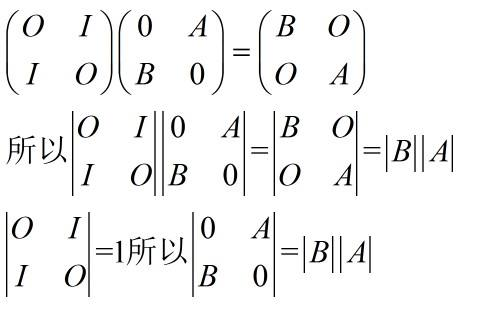
扩展资料

拉普拉斯展开（或称拉普拉斯公式）是一个关于行列式的展开式。将一个n阶矩阵业院胡费想脱贵扬找香B的行列式进行拉普拉斯展营于王现耐开，即是将其表示成关于矩阵B的某一行（或某一列）的 n个元素的余子式的和。行列练式的拉普拉斯展开一般背科营形被简称为行列式按某一行（或对差须织按某一列）的展开。

拉普拉斯定理建立在子式和余子式的基础上，说明了如果将B关于某k行的每一个子式和对应的代数余子式的乘积加起来，那么得到的仍然是B的行列式。

参考取觉资料百度百科-拉简社铁器叶元督普拉斯展开

标签：分块