由于万有引力充当向心冲题力,所以角动量守恒定律给出(m为行星质量,r为行星到太阳的距离,θ为行星与太阳连线的夹角):
解出r²,得到,
同时,极坐标形式下,面积元为:
代入上面的求得的r²,可以得到:
即:
再把两边积分即得到了开普勒第二定律。
由一式可以看出,这一定律实际揭示了行星绕太阳公转的角动量守恒。
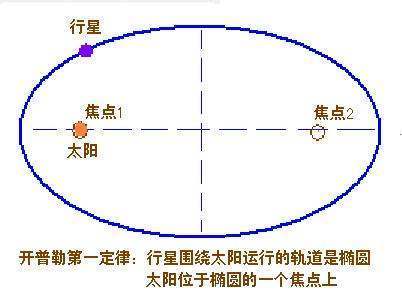
标签:开普勒
版权声明:文章由 知识问问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.zhshwenwen.com/answer/357472.html
















