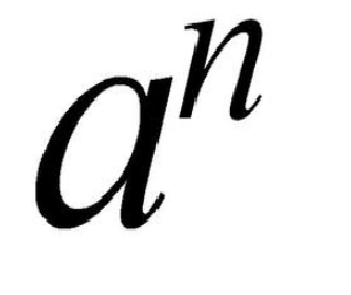分式的乘方和乘方法则

一、分式的乘方和乘方法则

1、分式的乘除

（1）乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母。

用式子表示为ab⋅cd=a⋅cb⋅dab·cd=a·cb·d。

（2）除法法则：分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘。

用式子表示为ab÷cd=ab⋅dc=a⋅db⋅cab÷cd=ab·dc=a·db·c。

（3）乘方法则：一般地，当nn是正整数时，

(ab)n=(ab)n=ab⋅ab⋅⋯⋅abn个=ab·ab·⋯·ab⏟n个=n个a⋅a⋅⋯⋅ab⋅b⋅⋯⋅bn个=n个a·a·⋯·ab·b·⋯·b⏟n个⏞=anbnanbn，即(ab)n=anbn(ab)n=anbn。

即分式乘方要把分子、分母分别乘方。

2、分式的加减

类似分数的加减，分式的加减法则是

（1）同分母分式相加减，分母不变，把分子相加减。

即：ac±bc=a±bcac±bc=a±bc。

（2）异分母分式相加减，先通分，变为同分母的分式，再加减。

即：ab±cd=adbd±bcbd=ad±bcbdab±cd=adbd±bcbd=ad±bcbd。

二、分式的乘方的相关例题

x2−1x+1⋅x2−xx2−2x+1=x2−1x+1·x2−xx2−2x+1=___

A．xx B．2x2x C．x2x2 D．2x22x2答案：A

解析：原式=(x+1)(x−1)x+1⋅x(x−1)(x−1)2=x=(x+1)(x−1)x+1·x(x−1)(x−1)2=x。故选A 。

标签：乘方